最近重温结城浩的《程序员的数学》,感触颇深。数学的应用广泛不言而喻,我们在平时的生活中离不开数学, 而作为搞开发的人来说,数学更是重中之重,这套书从基础的数学到概率统计,线性数学介绍了我们在日常开发中可能碰到的实例。
逻辑
真与假的二元世界
德摩根定律
- !A 或 !B == !(A 和 B)
- !A 和 !B == !(A 或 B)
余数
周期性与分组
今天是星期天,100天之后是星期几?
运用余数思考,100天以后就是“100除以7的余数”
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 日 | 一 | 二 | 三 | 四 | 五 | 六 |
100 % 7 = 2
所以100天以后是星期二
今天是星期天,10¹⁰⁰天以后是星期几?
由于数字比较大,我们用余数来计算也变得比较费事,我们可以尝试寻找其它的规律: 如1,10,100,1000,10000……这样,依次增加0的个数,观察其规律:
| 0的个数 | 天数 | 余数 | 星期 |
|---|---|---|---|
| 0 | 1 | 1 % 7 = 1 | 一 |
| 1 | 10 | 10 % 7 = 3 | 三 |
| 2 | 100 | 100 % 7 = 2 | 二 |
| 3 | 1000 | 1000 % 7 = 6 | 六 |
| 4 | 10000 | 10000 % 7 = 4 | 四 |
| 5 | 100000 | 100000 % 7 = 5 | 五 |
| 6 | 1000000 | 1000000 % 7 = 1 | 一 |
| 7 | 10000000 | 10000000 % 7 = 3 | 三 |
| 8 | 100000000 | 100000000 % 7 = 2 | 二 |
| 9 | 1000000000 | 1000000000 % 7 = 6 | 六 |
| 10 | 10000000000 | 10000000000 % 7 = 4 | 四 |
| 11 | 100000000000 | 100000000000 % 7 = 5 | 五 |
很明显的规律:
| 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 一 | 三 | 二 | 六 | 四 | 五 |
也就是说,每增加6个0,星期数就相同,因此周期为6。将0的个数除以6,得到的余数所对应的星期数即为所求。
那回到题目10¹⁰⁰天后是星期几?
100 % 6 = 4
则10¹⁰⁰天后是星期四。
涉及大数值是,如果不能直接计算,先尝试用较小的数字试算,找到规律,然后可能的话,在用余数计算。
运用余数,大数字的问题,就能简化成小数字的问题。
奇偶校验
奇偶校验在通信领域运用非常广泛,其实是将问题简化,分成2组。
最经典的就属:
哥尼斯堡七桥问题和欧拉猜想(一笔画的问题)
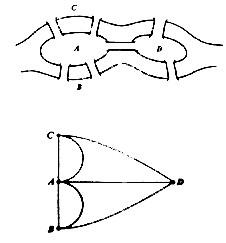
如果能够一笔画成,必须满足所有的顶点都是偶点或者只有2个奇点。
高斯求和
1 + 2 + 3 + 4 + … + n = ?
高斯断言
0到n的正数之和为 \[G(n) = \frac{n (n + 1)}{2}\]
排列(Permulation)
从n中取出k个按一定的顺序排列 \[P_{n}^{k} = \frac{n!}{(n - k)!}\]
组合(Combination)
从n中取出k个,不考虑顺序 \[C_{n}^{k} = \frac{P_{n}^{k}}{P_{k}^{k}} = \frac{\frac{n!}{(n-k)!}}{k!} = \frac{n!}{(n-k)!}\frac{1}{k!} = \frac{n!}{(n-k)!k!}\]
递归
汉诺塔
三根细柱A,B和C,A上面有n个圆盘,最终全部移到B(每次移到1个,小圆盘上面不能放大圆盘)
递归分析
- 首先将(n-1)个圆盘先移到C上。
- 将第n个圆盘移到B上。
- 然后将C上的(n-1)个圆盘移到B上,完成。
可以得到递归关系如下: \[H(n) = \begin{cases} 0 & \text{ ( } n= 0) \\ H(n-1) + 1 + H(n -1) & \text{ (} n= 1, 2, 3...) \end{cases}\]
解析式优化
从上面的H(0), H(1), H(2), … H(n)的结果,可以进一步的抽象出H(n)。
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
|---|---|---|---|---|---|---|---|
| 0 | 1 | 3 | 7 | 15 | 31 | 63 | … |
即可以用: \[H(n) = 2 ^ n - 1\]
阶乘的递归
同样的,阶乘用递归可以表述为: \[n! = \begin{cases} 1 & \text{ ( } n= 0) \\ n (n - 1)! & \text{ (} n= 1, 2, 3...) \end{cases}\]
斐波那契数列
有1种动物,它出生2天后就开始以每天1只的速度繁殖后代。假设第1天有1只这样的动物,到第n天共有多少只?
分析
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | … |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | … |
结论 \[F(n) = \begin{cases} 1 & \text{ ( } n <= 2) \\ F(n-1) + F(n-2) & \text{ (} n > 2) \end{cases}\]
指数爆炸
假设有一张厚度为1mm的纸,非常柔软,可以对折无数次,每对折一次,厚度就翻一番。已知地球距月球的距离是39万公里,请问对折多少次后厚度能超过地月距离呢?
如果没有计算过,数字绝对让你想不到……
| 1 | 2 | 10 | 20 | 30 | 38 | 39 |
|---|---|---|---|---|---|---|
| 2mm | 4mm | 1024mm | 1048.576m | 1073.741824km | 274877.906944km | 549755.813888km |
答案是39,没错,这就是指数爆炸。
二分查找法(Binary Search)
二分法在计算机中常用的查找数据的方法,其目的是在有序的数据中找出目标数据,其核心是“总是判断目标数据所在范围内的正中间的数据”。
二分查找法也正是使用了“指数爆炸”的方法,所以在大量的数据查找中,威力巨大。也就是说,每判断一次就能筛选出近一半的查找对象。
对数(Logarithm)
如果: \[A = 10^n\]
那么: \[log_{10}A = n\]
指数法则
\[10^a * 10^b = 10^{a + b}\]对数法则
\[log_{10}(A * B) = log_{10}A + log_{10}B\]总结
对于涉及指数爆炸的问题,大体上有四种处理方法。
极力求解
知道方法以后极力求解,即增强计算机性能,使用超级计算机或更先进的计算机来计算。
变相求解
换成简单问题来求解,即寻找更好的解法或算法。
近似求解
不求完全解答,而是找出近似解。
概率求解
有效使用随机数,在短时间内解决难题。
学生:老师,我的人生出现了360度的大转弯呢!
老师:360度的话,不就是没发生变化吗?
